Motivation

Sensitive information may need to be stored confidentially and also reliably. Storing the information in one secure location may provide confidentiality but not reliability. Replicating the information across multiple locations increases reliability but lowers confidentiality.

Secret sharing was invented independently by Shamir (1979) [6] and Blakeley (1979) [2]. It is a method in which information is split into several pieces and is reconstructed only by collecting at least a certain number of pieces. In the typical setting of a secret sharing scheme, a dealer distributes shares of the secret information among players. When a large enough subset of players convenes and fulfills certain conditions, they can reconstruct the original secret.

\((n,t)\)-secret sharing

We would like a dealer \(\mathcal{D}\) to generate shares \(\{s_i\}_1^n\) of a secret \(s\) and distribute them among \(n\) players \(\{\mathcal{P}_i\}_1^{n}\) obeying the following conditions.

1. Knowing any subset of \(\tau \leq t-1\) shares \(\{s_{i_j}\}_{j=1}^{\tau}\) leaks no information about \(s\).
2. Knowing any (sub)set of \(\tau\geq t\) shares \(\{s_{i_j}\}_{j=1}^\tau\) allows reconstruction of \(s\).

\(t\) is referred to as the tolerance or threshold of the scheme, and the participants in such a scheme are the dealer \(\mathcal{D}\) and the players \(\{\mathcal{P}_i\}_1^n\).

The first condition is similar to the condition of perfect secrecy for an encryption scheme. In other words, for a distribution of \(s\) over the space of secrets, we would like $$\text{Pr}[s=s_0 \mid s_{d_1},...,s_{d_{t-1}}]=\text{Pr}[s=s_0]$$

A secret sharing scheme has two consecutive phases.

1. In the sharing phase, \(\mathcal{D}\) sends each \(\mathcal{P}_i\) a share \(s_i\) that is unknown to other players \(\mathcal{P}_{j\neq i}\).
2. In the reconstruction phase, the players pool shares to recover \(s\).

We treat each \(s_i\) as a parameterized equation \(s_i = f_s(x_i)\) where any set of \(t-1\) or fewer such equations has infinitely many solutions, and any set of at least \(t\) such equations has solution \(s\).

Setup

We embed \(s\) in the Galois field \(\mathbb{Z}_p\), the set of integers modulo a large prime \(p\). Henceforth, we assume all numbers and operations are set in this field, and that "random" elements are chosen uniformly at random from this field (denoted as \(x\leftarrow\mathbb{Z}_p\)) unless otherwise specified.

The network consists of players which are probabilistic and polynomial-time (PPT) algorithms. Each player can access a private channel with every other player, as well as a common broadcast channel to the entire network (including the dealer). In future sections, we will examine the potential for dishonesty due to corruption among participants. We assume adversaries are also PPT algorithms that can monitor broadcast channels. Adversaries are not necessarily players, and seek access to a player's state by corrupting that player. We refer to corrupted players as dishonest and assume that less than half of all players are dishonest.

\((n,t)\)-SSS

In Shamir's secret sharing (SSS), as proposed in Shamir (1979) [6], the secret \(s\) is an element \(a_0\in\mathbb{Z}_p\). Coefficients \(\{a_i\}_{i=1}^{t-1}\) are chosen uniformly at random from this field to construct the polynomial $$q(x) = \sum_{i=0}^{t-1}a_ix^i$$

Assuming that players know their index \(i\), each player \(\mathcal{P}_i\) has private information constituting a point \((i,s_i=q(i))\) on the polynomial. This assumption is convenient as it allows us to regard a share as a value \(s_i\) rather than a point \((i,s_i)\). So, the shares are \(\{s_i=q(i)\}_1^n\).

In the sharing phase, \(\mathcal{D}\) sends each \(\mathcal{P}_i\) a share \(s_i\) that is unknown to other players \(\mathcal{P}_{j\neq i}\). In the reconstruction phase, the players try to recover the secret \(s=q(0)=a_0\) using a technique called Lagrange interpolation.

We refer to Scheme 1 as "\((n,t)\)-SSS", "SSS", "Shamir's secret sharing", or "Shamir's scheme" interchangeably.

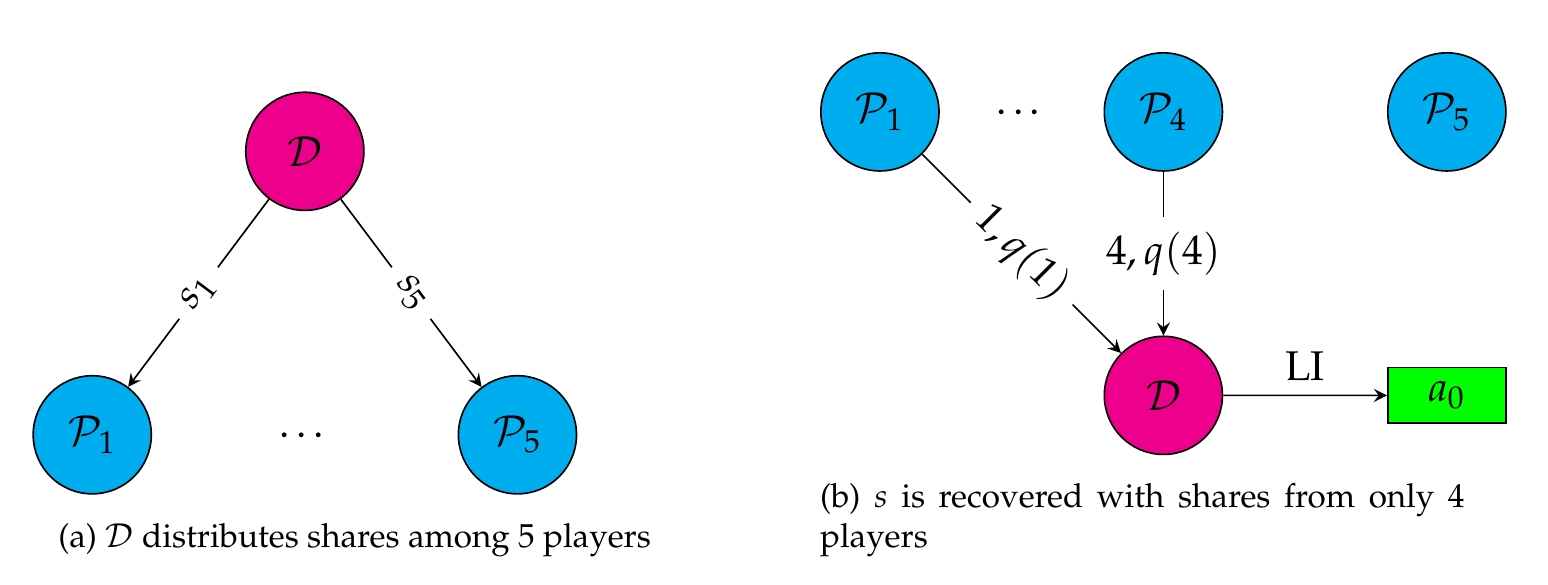
Lagrange interpolation

Shamir's scheme is correct since knowledge of \(t\) points allows reconstruction of \(a_0\) using polynomial interpolation over a finite field. If \(t=n\), then players simply need every share \(s_i\) to compute $$\sum_{i=1}^ts_i\prod_{j\neq i}\frac{-j}{i-j}=\sum_{i=1}^tq(i)\prod_{j\neq i}\frac{-j}{i-j}=q(0)$$ The Lagrange coefficients \(\lambda_i=\prod_{j\neq i}\frac{-j}{i-j}\) can be computed ahead of time in the interest of efficiency.

While the \(n=t\) case does illustrate interpolation, it ignores threshold cryptography. We typically have \(t<n\), and so we expect differences between the total number of shares, the number of pooled shares, and the number of shares that reconstruct the secret. Hence, we say that out of the pooled shares, some \(t\) shares \(\{s_{d_i}\}_{i=1}^{t}\) are enough to reconstruct the secret as $$\sum_{i=1}^{t} s_{d_i} \lambda_{d_i}=\sum_{i=1}^{t} q(d_i)\lambda_{d_i}=q(0)$$

Shamir's scheme achieves the desired security because no subset of \(t-1\) or fewer points leaks any information about \(a_0\). Suppose we have an instance of Shamir's scheme with such a subset \(\{(i_j,s_{i_j})\}_{j=1}^{t-1}\) of points on \(q(x)\). Then for each index \(j\), every polynomial \(\kappa(x)\) with degree \(t-1\) and having constant term \(a_0=s\) also satisfies \(\kappa(j)=s_j\).

In addition to the security guarantees provided by threshold cryptography, there are numerous other benefits to Shamir's scheme. Frequently updating the shares can greatly enhance security as it provides less time for an adversary to corrupt enough players to accumulate the necessary shares to meet the threshold. Under Shamir's scheme, it is simple to update shares without changing the original secret: simply find a new polynomial with the same \(a_0\) term. Shamir's scheme is also proportional with hierarchies, as players can hold more or fewer shares according to their rank (although we assume here that each player receives only one share).

However, SSS has a major problem: it assumes that participants of the scheme are honest, meaning that the dealer and players are not malicious and do not attempt to subvert the scheme. This is an unqualified assumption, and so we move to schemes that add a layer of verifiability on top of SSS.

Another problem is that of authentication: players should have assurance that shares originated with the dealer and not with some other party. This can be addressed by delayed information transmission and information checking, which we omit here. However, even with authentication, the issues related to a dishonest dealer still remain, as a dishonest dealer may send authenticated yet faulty shares. Such scenarios motivate attempts to safeguard against dishonest dealers in addition to dishonest players.

Verifiability from commitments

With SSS, there is no guarantee that any subset of shares defines the secret \(s\). This provides an attack vector for adversaries and dilutes faith in the scheme among participants. The two main issues with SSS are as follows.

Firstly, a dishonest \(\mathcal{D}\) can distribute shares belonging to different polynomials, resulting in different combinations of players reconstructing different secrets. Hence, the scheme may be rigged in favor of certain players or it may not even be meaningful. Players need assurance that their shares are from a single polynomial, and \(\mathcal{D}\) needs assurance that honest players will accept the generated shares.

Secondly, dishonest players can submit fake shares in order to impede reconstruction. The dealer may generate all shares from the same polynomial \(q\), but some players may still reveal shares from a different polynomial \(\kappa\). Different combinations of \(t\) shares can result in different secrets. So, we need a way to check the correctness of revealed shares.

These two issues form the motivation for verifiable secret sharing (VSS). The goal of VSS is to ensure that the shares distributed by the dealer define a secret and will be accepted by honest players.

When considering the possibility of a dishonest dealer, we can frame secret sharing as a commitment in which the dealer commits to a value. Some verifying party can verify these commitments. Because a dishonest dealer has far more power to abuse a scheme than a dishonest player, we are more concerned with the former scenario than the latter. Hence, in VSS we require the dealer to publish commitments on distributed shares. In VSS, the player \(\mathcal{P}_v\) verifies only the commitment corresponding to \(s_v\). In publicly verifiable secret sharing, the verifying party \(\mathcal{V}\) has vastly more freedom.

At the start of the sharing phase, if \(\mathcal{D}\) is honest then it has a secret \(s\) that the players do not know. At the end of the sharing phase, we would like to have correctness. The reconstruction phase is executed after the sharing phase has completed, and we would like reconstruction to achieve termination and secrecy. These goals are as follows.

1. Correctness: honest players can output the secret at the end of the reconstruction phase.
2. Termination: if all honest players invoke reconstruction, then all honest players complete reconstruction.
3. Secrecy: if the dealer is honest and the the reconstruction phase has not been started by honest players, then the dishonest players learn nothing about the secret.

We now move toward verifiable secret sharing based on homomorphic functions.

Homomorphic \((n,t)\)-VSS

Homomorphic secret sharing was introduced by Benaloh (1986) [1] as a way to perform secret sharing on a super-secret \(s=s^{(1)} * s^{(2)}\) composed of sub-secrets \(s^{(1)}, s^{(2)}\), while revealing as little information about the sub-secrets as possible during reconstruction. In a primitive version of such a scheme, \(\mathcal{D}\) would hold the super-secret \(s\) and distribute sub-shares \(s^{(1)}_i, s^{(2)}_i\) to each \(\mathcal{P}_i\), who would then pool the super-share \(s_i=s^{(1)}_i \circ s^{(2)}_i\) to reconstruct the super-secret.

Notice the homomorphic property at play in this scenario: the composition of shares of secrets is a share of the composition of secrets. The symbols \(*, \circ\) denote arbitrary operations.

Homomorphic secret sharing combines the desirable properties of homomorphic functions with secret sharing, and its desirable properties are the reason for its popularity among electronic voting schemes. However, it does not on its own provide verifiability.

We now study a variant of a VSS scheme due to Feldman (1987) [3] that provides verifiability on a homomorphic secret sharing scheme. We modify the verification subprotocol in Feldman's scheme so that it follows an interactive zero-knowledge protocol. This variant is similar to the one presented in Katz and Lindell (2007) [4]. Feldman's original scheme uses a non-interactive protocol, which is desirable under certain network conditions. The original also allows players to act as dealer in order to achieve parallel secret sharing. In the PVSS setting, we will move to non-interactive protocols.

The goal of this VSS scheme, as with all VSS schemes, is to achieve correctness, termination, and secrecy.

The idea of Feldman's scheme is to use homomorphic relationships that may exist between values and their encryptions. As a preliminary, we select a large prime factor \(\rho\) of \(p-1\) in order to conduct Shamir's scheme over the field \(\mathbb{Z}_{\rho}\) with generator \(g\). \(\mathcal{D}\) distributes shares as in \((n,t)\)-Shamir's secret sharing. \(\mathcal{D}\) broadcasts some values \(\{\sigma_i\}_0^{t-1}\), where \(\sigma_i=g^{a_i}\). Observe that $$\prod_{j=0}^{t-1}(\sigma_j)^{i^j}=\prod_{j=0}^{t-1}(g^{a_j})^{i^j}=(g^{a_0})(g^{a_1})^{i}...(g^{a_{t-1}})^{i^{t-1}}=g^{\sum_{j=0}^{t-1}a_ji^j} =g^{q(i)}$$ where \(q(x)=\sum_{i=0}^{t-1}a_ix_i\) is the polynomial from Shamir's scheme. Players verify the correctness of their received shares by using public and private information to evaluate \(g^{s_i}\stackrel{?}{=} \prod_{j=0}^{t-1}(\sigma_j)^{i^j}\).

In Feldman's scheme, it is not the case that \(s=q(0)=a_0\), as in Shamir's scheme. Simply by the nature of polynomials, it is true that \(q(0)=a_0\). However, the secret \(s\) is distinct from \(a_0\) in this scheme. Players receive shares of \(a_0\), reconstruct \(a_0\), and use a public value \(c\) to reconstruct \(s\) as \(s=H(a_0)\oplus c\).

Note that with honest \(\mathcal{D}\), every share passes verification.

Termination is clear. Regarding correctness, if the dealer is not disqualified, then the reconstructed value is \(c\oplus H(\text{log}_g \sigma_0)\). Regarding secrecy, dishonest players learn no additional information due to the hardness of the discrete logarithm problem: the secret is masked by the random value \(H(a_0)\), and the information shared with players—shares \(\{s_i\}_1^n\) and values \(\{\sigma_i\}_0^{t-1}\)—reveals only \(g^{a_0}\), not \(a_0\).

So far, we have examined VSS schemes in which the verification is done by participants of the protocol, whether they are players or the dealer. But this presents some limitations. A VSS scheme does not prescribe a method for meting punishment; it merely indicates that certain parties have behaved dishonestly. Punishment is extraneous to the scheme, and can be avoided by an adversary who succeeds in a sufficiently large-scale attack even on a network that enacts a VSS instance.

To avoid such a scenario, certain networks may benefit from a VSS scheme with enhanced verification, in which a verifier \(\mathcal{V}\) can verify a share \(s_i\) even if \(\mathcal{V}\neq\mathcal{P}_i\). Such schemes are referred to as publicly verifiable secret sharing (PVSS) schemes, and their goal is to ensure that the honesty of \(\mathcal{D}\) can be verified publicly. A verifier may be a player checking the share of another player, or it may be some extraneous party.

The benefits of PVSS range from enhanced security to enhanced confidence in the network by non-participants. Since other parties can verify a player's share with PVSS, a player who intentionally submits an incorrect share during reconstruction does so with the risk of being found out. Some interesting game-theoretic scenarios arise from this risk, but we don't pursue them here. Moreover, players are free to leave verification to other parties, and no longer bear the computational weight of verifying their own shares or broadcasting complaints. Applications such as electronic voting, digital payments, or escrow transactions could make great use of such systems.

Asymmetric encryption on VSS

\((n,t)\)-PVSS with double discrete logarithms

Using an asymmetric encryption scheme \((\text{KeyGen}, \mathrm{Enc_{pub}}, \mathrm{Dec_{sec}})\) on top of a secret sharing scheme produces the innovation of PVSS over VSS. \(\mathcal{D}\) publishes \(\mathrm{Enc_{pub}}(s_i)\) for each share as well as a string \(\text{Proof}(\mathrm{Enc_{pub}}(s_i))\) that commits \(\mathcal{D}\) to the value of \(s_i\). A verifier \(\mathcal{V}\) runs a verification algorithm on each \(\text{Proof}(\mathrm{Enc_{pub}}(s_i))\) to verify that \(\mathrm{Enc_{pub}}(s_i)\) is a correct encryption of \(s_i\). Alternatively, \(\mathcal{V}\) may request a proof corresponding to only a particular share \(s_v\). Regardless of the number of requested verifications, the commitments must be made on all players. Any party may verify share \(s_i\) with knowledge of the corresponding public key.

Given an honest dealer, honest players can decrypt \(\tau\geq t\) shares that pass the public verification algorithm to recover the secret. If all shares pass public verification, then the output \(r\) of reconstruction equals the secret \(s\).

Verification may or may not require interaction with the dealer. The proposed public verification protocols constitute zero-knowledge proofs.

We study the PVSS scheme due to Stadler (1996) [7], which introduced PVSS. The scheme relies on the hardness of the double discrete logarithm problem, which is a variant of the DLP. A double discrete logarithm is the unique value \(x\in\mathbb{Z}_q\) where \(y=g^{(h^x)}\) for a given group element \(y\) and bases \(g, h\).

The encryption scheme used in this protocol is very similar to the ElGamal cryptosystem and Diffie-Hellman key exchange.

The verifier \(\mathcal{V}\) can be any party who has knowledge of the public keys. \(\mathcal{V}\)'s goal is to check the correctness of a share \(s_v\) using knowledge of the encrypted share \(S_v\), which \(\mathcal{V}\) views as a tuple \((A,B)\). The prover, \(\mathcal{D}\), engages \(\mathcal{V}\) in an interactive protocol to produce a proof tuple \((W,S)\) such that decrypting \(W\) yields \(\log_{\,g} S\).

With a few steps of substitution, it is easily provable that the check in the verification subprotocol passes if no values are altered. Checking the equality at the \(i\)-th bit is as follows: $$ \begin{align*} c_i=0&\implies \begin{cases}h^{r_i}A^{c_i}=h^{w-c_i\alpha}=h^w=t_h\\ (g^{1-c_i}\sigma_v^{c_iB})^{(y^r)}=g^{(y^{r_i})}=g^{(y^w)}=t_g \end{cases}\\ c_i=1&\implies \begin{cases}h^{r_i}A^{c_i}=h^{w-\alpha}h^\alpha=h^w=t_h\\ (g^{1-c_i}\sigma_v^{c_iB})^{(y^{r_i})}=(\sigma_v^B)^{(y^{r_i})}=(g^{(y^\alpha)})^{(y^{r_i})}=g^{(y^w)}=t_g\end{cases} \end{align*} $$

Termination of this protocol is clear, since the protocol either aborts if not enough honest players remain, or outputs a reconstructed value if the threshold of players is met. The verification subprotocol and Lagrange interpolation provide assurance of correctness. Regarding secrecy, determining \(s_i\) from knowledge of \(g^{s_i}\) and \((h^\alpha, s_i^{-1}y_i^\alpha)\) reduces to solving the Diffie-Hellman problem with base \(h\).

In the verification subprotocol, \(\mathcal{D}\) as the prover can successfully cheat with negligible probability \(<2^{-l}\).

\((n,t)\)-PVSS with player commitments

In Stadler (1996), players need only pool their shares in order to reconstruct \(s\). More robustness could be achieved if players also were to publish a proof that the share they submit for reconstruction is correct. Stadler's scheme also relies on a non-standard assumption, which is the hardness of double discrete logarithms. These issues are addressed in Schoenmakers (1999) [5], which proposes a scheme based on the Diffie-Hellman assumption that requires commitments by both the dealer and by the players. We now study Schoenmaker's scheme, and then proceed to an application to electronic voting.

This scheme adds another feature to our model for PVSS. In reconstruction, players decrypt a subset of shares from \(\{\mathrm{Enc_{pub}}(s_i)\}_1^n\). Each player \(\mathcal{P}_i\) pools its decrypted share and also publishes a proof committing itself to the pooled, decrypted share. If this proof is found to be invalid, then \(\mathcal{P}_i\)'s pooled share is excluded and the reconstruction continues with the set of valid shares. Similar to the proof for a distributed share (encryption), the proof of a pooled share (decryption) also follows a non-interactive protocol.

Additionally, players in this scheme do not learn their share. In the sharing phase, \(\mathcal{D}\) generates a polynomial \(q\) as per Shamir's scheme but sets the secret as \(s=h^{q(0)}\) rather than to \(q(0)\). Even though the shares are still consistent with Shamir's scheme (\(s_i=q(i)\)), each player \(\mathcal{P}_i\) only learns a value \(h^{s_i}\). This does not present a challenge to the goals of correctness, termination, and secrecy. Verifiability and integrity do not depend on players learning the value of their share.

Observe that this scheme can be viewed as either \((+,+)\)-homomorphic or \((\times,\times)\)-homomorphic, since shares of sub-secrets \(s^{(1)}=h^{q(0)}, s^{(2)}=h^{\kappa(0)}\) can be used to reconstruct the super-secret \(s=h^{q(0)+\kappa(0)}\) by reconstructing with the encrypted super-shares as \(S_i^{(1)}S_i^{(2)}=y_i^{s_i^{(1)}+s_i^{(2)}}\).

This scheme reduces work from \(\mathcal{O}(\mu^2 n)\) in Stadler's scheme to \(\mathcal{O}(\mu n)\) for security parameter \(\mu\).

Elections on \((n,t)\)-PVSS

An electronic voting scheme has players \(\{\mathcal{P}_i\}_1^n\) that make up the two (possibly overlapping) sets of casters \(\{\mathcal{C}_j\}_1^l\) and talliers \(\{\mathcal{T}_k\}_1^m\). The election protocol has two phases:

1. In the casting phase, each \(\mathcal{C}_j\) publishes its ballot using a sharing subprotocol from PVSS.
2. In the *tallying* phase, the talliers collectively compute the tally of votes using a reconstruction subprotocol from PVSS.

Each caster acts as a dealer, and each tallier acts as a player from secret sharing. We refer to an encrypted binary vote as a ballot.

A further verification subprotocol can be embedded in this scheme for verifying whether \(\omega_v \in \{0,1\}\) via a proof that \(\log_{\,h}U_v\in\{\log_{\,g}\sigma_0, 1 + \log_{\,g}\sigma_0\}\).

In Schoenmakers (1999) [5], step 6 is vague about how \(\mathcal{T}_k\) goes about accumulating the values \(\{q_j(k)\}_{j=1}^m\). Clearly, publishing the polynomials \(q_j\) in the PVSS scheme would reveal the secret. In the worst case where \(n=m=l\), each tallier would need \(n-1\) rounds of communication over private channels to accumulate those values, leading to nearly \(n^2\) rounds of communication overall for that one step.

This election scheme has the benefit of not requiring shared key generation among talliers.

In developing an understanding of secret sharing, we have examined threshold cryptography, homomorphic encryption, asymmetric cryptosystems, and verifiability, at the intersection of which we find this electronic voting application. Further extensions could involve examining the information-theoretic tradeoffs as well as the practicality of the schemes we have discussed.

References

1. Benaloh, Josh Cohen. 1986. “Secret Sharing Homomorphisms: Keeping Shares of a Secret Sharing.” In Advances in Cryptology - CRYPTO '86, 263:251–60. Lecture Notes in Computer Science. Springer. https://link.springer.com/chapter/10.1007/3-540-47721-7_19
2. Blakley, G. R. 1979. “Safeguarding Cryptographic Keys.” In Proceedings of the 1979 AFIPS National Computer Conference, 313–17. AFIPS Press.
3. Feldman, Paul. 1987. “A Practical Scheme for Non-Interactive Verifiable Secret Sharing.” In 28th Annual Symposium on Foundations of Computer Science (Sfcs 1987), 427–38. https://doi.org/10.1109/SFCS.1987.4.
4. Katz, Jonathan, and Yehuda Lindell. 2007. Introduction to Modern Cryptography. Chapman; Hall/CRC Press.
5. Schoenmakers, Berry. 1999. “A Simple Publicly Verifiable Secret Sharing Scheme and Its Application to Electronic Voting.” In Advances in Cryptology - CRYPTO '99, 148–64. Lecture Notes in Computer Science, vol 1666. Springer.
6. Shamir, Adi. 1979. “How to Share a Secret.” In Communications of the ACM 22 (11): 612–13.
7. Stadler, Markus. 1996. “Publicly Verifiable Secret Sharing.” In Advances in Cryptology — EUROCRYPT ’96, 190–99.