Acronyms

• CFT: Continuous Fourier transform
• DFT: Discrete Fourier transform
• FFT: Fast Fourier transform
• CNN: Convolutional neural network
• FCNN: Fourier convolutional neural network

Introduction

The Fourier transform is a powerful tool for transforming a time-domain function into a frequency-domain function. We dive into the mathematical and the computing aspects of the fast Fourier transform (FFT), an algorithm to efficiently compute the discrete Fourier transform (DFT). We then tie the FFT in with its use in convolutional neural networks (CNNs). Sorry, no NFT!

For background knowledge on the Fourier transform, this 3Blue1Brown video is excellent.

Fourier transform

The Schwartz space over the reals is denoted as \(\mathcal{S}(\mathbb{R})\).

We denote any Fourier transform—whether continuous, discrete, multi-dimensional, etc.—by \(\mathcal{F}\) throughout, with the particular form readily apparent from context.

The continuous Fourier transform (CFT) has many nice properties including linearity and shift invariance. We don't prove the many amazing properties of the CFT, as that deserves an entire book in its own right.

In the real world, we are often concerned with discrete signals. Hence, we need a discrete analogue of the CFT. The DFT allows the study of continuous functions through sampling and extends Fourier theory to inherently discrete signals such as trading activity on the stock market.

The need for the DFT highlights a fundamental difference between mathematics and computing. Whereas mathematics can deal with behaviors over domains such as all of time or \(\mathbb{R}^N\), computers must work over discrete domains. In fact, discrete domains pervade all realms of science due to the nature of sampling. Moreover, computers require a finite amount of data and so cannot even algorithmically implement the CFT. These reasons have given the DFT tremendous importance in image and digital signal processing.

As the DFT is a linear function on \(\mathbb{R}^N\), we can express it as a matrix. Observe that we can write some \(j\)-th entry \(\mathcal{F}(x)_j\) as $$x_0 + x_1 \cdot e^{-2 \pi ij/N} + \ldots + x_{N-1} \cdot e^{-2(N-1) \pi ij/n}$$ This equality is the result of the dot product $$\begin{bmatrix}1&e^{-2\pi ij/N}&\ldots &e^{-2(N-1)\pi ij/N}\end{bmatrix}\cdot\begin{bmatrix}x_0 \\ x_1 \\ \vdots \\ x_{N-1}\end{bmatrix}$$ So, we may write the DFT as the linear transformation $$\begin{bmatrix}\mathcal{F}(x)_0&\mathcal{F}(x)_1&...&\mathcal{F}(x)_{N-1}\end{bmatrix} = \\ \begin{bmatrix} 1&1&...&1 \\ 1&e^{-2 \pi i/N}&...&e^{-2(N-1) \pi i/N} \\ \vdots&\vdots&...&\vdots \\ 1&e^{-2 \pi i/N}&...&e^{-2(N-1) \pi i/N}\end{bmatrix}\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_{N-1}\end{bmatrix}$$

This representation of the DFT is particularly striking as it moves the understanding of the transform from integration over \(\mathbb{R}\) to a discrete sum and now to a matrix, allowing us to glimpse a method for computers to compute the DFT.

Notice that this matrix computation has \(\mathcal{O}(N^2)\) time complexity. With a large sample size, this computation proves to be naive. To meet the high-volume computing needs, the DFT must be computed much more quickly. The FFT was developed as a means of minimizing the amount of time it takes to compute the DFT.

Fast Fourier transform

Calculating the DFT directly is computationally infeasible in the vast majority of cases, which is why the DFT was rarely used before the popularization of the FFT. The development of the FFT can be traced back to Gauss, who described a similar algorithm in 1805. Remarkably, Gauss' work on this subject predated even Fourier's own work on harmonic analysis. However, Gauss did not publish this work in his lifetime [3].

The modern understanding of the FFT is attributed to Cooley and Tukey, who published the landmark algorithm in 1965. Cooley and Tukey's algorithm reduced the time complexity of the DFT from \(\mathcal{O}(N^2)\) to "less than \(2N\log N\) operations without requiring more data storage" [2]. Cooley and Tukey's algorithm made all manners of digital signal processing more efficient and thus feasibly computable. Though some other algorithms for calculating the DFT are also sometimes referred to as the FFT, Cooley and Tukey's is the one most commonly used.

For simplicity, let \(\omega_k = e^{-2 \pi i/k}\). We will show that the FFT's claimed improvement is realized when \(N\) is a power of \(2\). The FFT is a divide-and-conquer algorithm in that it recursively halves the required DFT computation until all that remains is a DFT with length \(1\). The proof Theorem 1 illustrates the FFT's speedup.

Higher-dimensional transforms

Many applications of the DFT and FFT occur in higher dimensions. As it turns out, the DFT in two dimensions is very similar to the 1-dimensional DFT.

The properties of linearity and translation invariance in the case of \(\mathbb{R}\) carry over to \(\mathbb{R}^N\). For simplicity, we stick with the 2D DFT which is a linear mapping from multi-dimensional matrices to multi-dimensional matrices.

As the 1D DFT decomposes a signal such as sound into a linear combination of its constituent sine and cosine waves, the 2D DFT decomposes an image into a frequency representation of pixel cycles. The intuition for the FFT in \(2\) dimensions is as follows.

Fixing some index \(n\), the corresponding inner summation of the DFT over some vector \(y\) is $$G(X)_{n,k} = \sum\limits_{m=0}^{M-1} X_{n,m} \cdot e^{-2 \pi i(my/M)}$$

Then, write the DFT of \(X\) as $$\mathcal{F}(X)_{j,k} = \sum\limits_{n=0}^{N-1} G(X)_{n,k}e^{-2\pi i(nj/N)}$$

Since \(n\) is fixed, \(\mathcal{F}(X)_{j,k}\) has the form of a 1D DFT.

The strategy is to fix each index \(0\leq n\leq N-1\) and to compute each resulting 1D DFT using the term \(G(X)_{n,k}\).

In this manner, the inner summations are \(\mathcal{O}(NM\log M)\) and the outer summations are \(\mathcal{O}(NM\log N)\) so that the 2D FFT requires \(\mathcal{O}(NM\log NM)\) operations.

Amazingly, this is the same time complexity as the 1D FFT!

Convolution

The convolution is a ubiquitous operation in Fourier analysis, and has broad use in many fields including in machine learning.

Due to the nature of the Schwartz space, the function \(f(x-y)g(y)\) rapidly decreases in \(y\) for a fixed value of \(x\). Hence, the integral converges.

The convolution is a useful operation to combine two functions in order to produce a third and has many nice properties including commutativity, associativity, distributivity, and scalar associativity. We are most interested in the convolution's relationship with the Fourier transform.

The convolution's discrete, finite analogue is the most useful operation in digital signal processing. It is tempting to naively translate the convolution into a discrete, finite version as something of the form $$(f*g)_j = \sum_{m=0}^{N-1}f_m\cdot g_{j-m}$$ for finite sequences \(f,g\in\mathbb{R}^N\), but the value of this naive convolution is unclear due to the ambiguity in indexing when \(m>j\). One solution is to to use periodic extensions to produce what is called a circular convolution.

Unsurprisingly, the discrete convolution has an analogous theorem with an analogous proof. The operator \(\odot\) denotes a Hadamard product, i.e. an entrywise product.

Convolutional neural networks work in higher dimensions, as they accept inputs in the form of tensors. So we need a formulation for higher-dimensional discrete convolutions.

Convolutional filtering

In image filtering, image data in tensor form is convolved with a kernel to transform the image values according to some filtering goal such as smoothing, sharpening, or edge detection. Using the formulation in Definition 6, the kernel is the tensor \(g\) and the image is the tensor \(f\). The terms kernel and filter are used interchangeably.

Implementations of the convolution may not conform perfectly to the formulation in Definition 6. In practice, the number of summations and the output size of a convolution depend on the choice of stride as well as the decision either to implement a circular convolution or to resort to padding. Additionally, the terms "convolutional layer" and "convolution neural networks" are misnomers, since they actually implement the cross-correlation operation. Cross-correlation, which is very similar to the convolution, has the form $$(f*_cg)_{n_1,n_2}=\sum_{m_1=0}^{K-1}\sum_{m_2=0}^{K-1}f_{n_1+m_1,n_2+m_2}\cdot g_{m_1,m_2}$$ in \(2\) dimensions, where the indices \(n_i-m_i\) are changed to \(n_i+m_i\). The summation is usually normalized by the sum of the kernel weights.

Another important point to note is the input rank. Definition 6 considers the general case. Practically, input tensors are characterized by three dimensions: height, width, and channel. An image consists of three channels (red, green, and blue). Thus, in a convolutional layer, the operation consists of three summations, with the third summation over the channel dimension.

For example, let's look at a couple of the steps in applying a smoothing (i.e., noise reduction) filter. Suppose we have the following matrix representing an isolated channel—the red pixel values—of some input image.

We have the following smoothing filter.

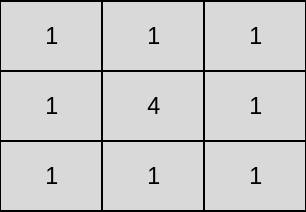
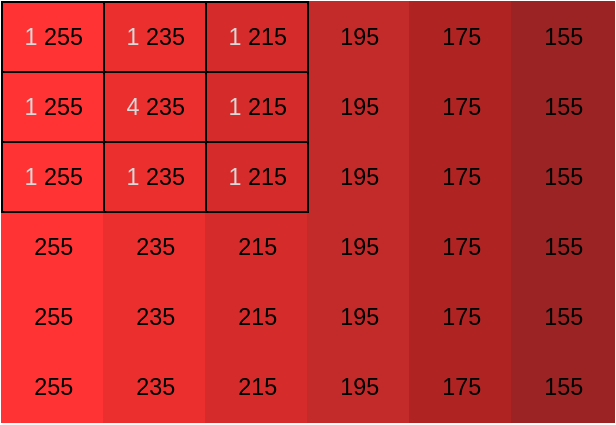
Note that \(f\) and \(g\) are matrices and hence tensors of rank \(2\). \(f\) has dimension \(6\) and \(g\) has dimension \(3\). In practice, the tensor dimension is massive.

Computing \((f*_cg)_{0,0}\) is straightforward. $$(f*_cg)_{0,0}=\frac{2820}{12}=235$$

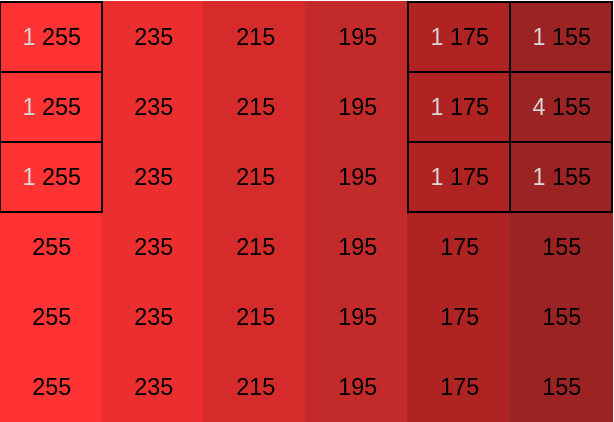
Computing \((f*_cg)_{0,4}\) is more interesting as it demonstrates the benefit of the circular convolution, which is the ability to wrap around the image as needed so that the final output has the same shape as the input. $$(f*_cg)_{0,4}=\frac{2220}{12}=185$$

Convolutional neural networks

Convolutional neural networks (CNNs) are a widely used class of neural networks in image processing and are implemented on GPUs. A major part of the objective with CNNs is to learn proper kernels, which is done using an algorithm called back-propagation. CNNs are feedforward networks since signal information moves unidirectionally.

CNNs have many different hidden layers, mainly convolutional layers but often also subsampling layers, pooling layers, and ReLU layers, among others.

A convolutional layer applies a convolution, using a filter of fixed size as described above, to transform the input pixel values. The number of kernels defines the number of feature maps (or channels), and the kernel dimensions define the receptive fields.

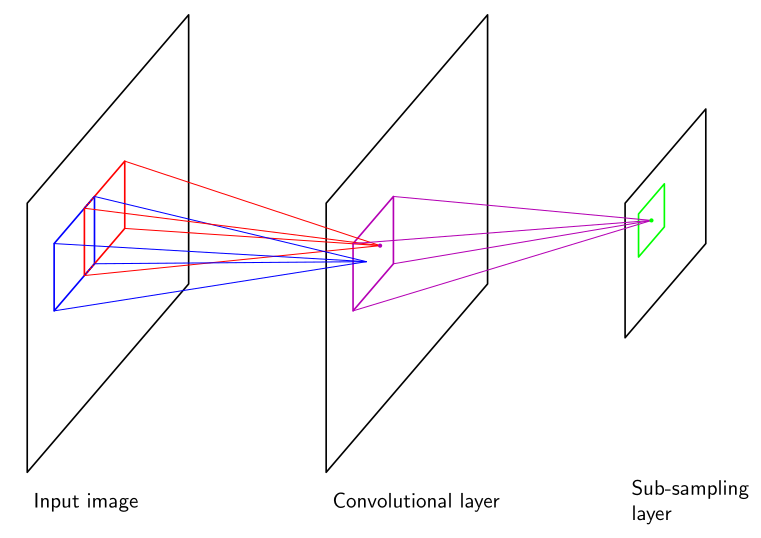
Outputs of the convolutional layers can be fed into subsampling layers. Each subsampling unit corresponds to a feature map in the preceding convolutional layer and performs subsampling on inputs from a small receptive field from that feature map. In other words, subsampling replaces a neighborhood of pixels a receptive field with a representative pixel. Pooling layers are conceptually similar to subsampling. In either subsampling or pooling, the process of feature extraction results in dimensionality reduction and thus less data. An example given by Bishop would "take inputs from a \(2\times 2\) unit region in the corresponding feature map and would compute the average of those inputs, multiplied by an adaptive weight with the addition of an adaptive bias parameter, and then transformed using a sigmoidal nonlinear activation function" [1]. Figure 1 illustrates the convolutional-subsampling relationship.

A ReLu layer applies an activation function such as \(\text{max}(0,x)\) element-wise, leaving dimensionality unaffected.

CNNs usually end with a fully connected layer, where the neurons are connected to all of preceding layer's neurons (as in an ordinary neural network). The output layer holds the input's classification and also computes an error (according to some loss function) which is distributed back to the hidden layers. It is this backpropagation of errors that allows weights to be updated and kernels to be learned.

We can deploy our own CNN on free-to-use GPUs thanks to Google Colab. Consider the following implementation of a CNN with a sequence of convolutional, max pooling, batch normalization, ReLu, and fully connected layers along with categorical cross-entropy loss. It uses keras to recognize digits from images provided by the SVHN dataset.

model = Sequential()
model.add(Conv2D(64, (5,5), activation='relu', input_shape=(32, 32, 3), padding='same'))
model.add(BatchNormalization())
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (5, 5), activation='relu', padding='same'))
model.add(BatchNormalization())
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(128, (5, 5), activation='relu', padding='same'))
model.add(BatchNormalization())
model.add(Flatten())
model.add(Dense(3072, activation='relu'))
model.add(Dense(2048, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))

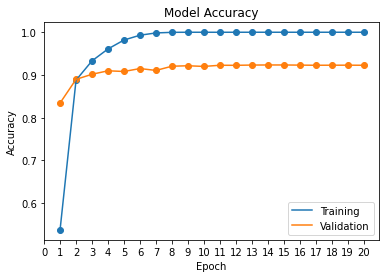
model.compile(loss=categorical_crossentropy, optimizer=gradient_descent_v2.SGD(learning_rate=0.1), metrics=['accuracy'])

Running the Colab script yields the model accuracy shown in Figure 2. An accuracy of approximately \(92\%\) isn't amazing, but it demonstrates how quickly and easily a model can be architected in the current machine learning landscape. We could certainly increase the accuracy with a few parameter tweaks.

Fourier CNNs

The convolution can be extremely costly in a CNN, especially with large images and kernels. Letting the image be a square matrix of size \(N\) and the kernel a square matrix of size \(M\), computing the convolution directly requires \(\mathcal{O}(N^2M^2)\) time. How can we speed this up?

We can use the discrete convolution theorem as well as the FFT to efficiently compute the convolution indirectly. We know by the discrete convolution theorem that a convolution \(f*_cg\) in a time or spatial domain corresponds to a Hadamard product \(\mathcal{F}(f)\odot\mathcal{F}(g)\) in the associated frequency domain via the DFT. With this representation in hand, we can work entirely in the frequency domain where we have an efficient algorithm: the FFT!

The FFT efficiently computes the individual components of the Hadamard product and the inverse Fourier transform of the product to yield a result equivalent to the convolution. Figure 3 illustrates the indirect computation of the convolution using the FFT.

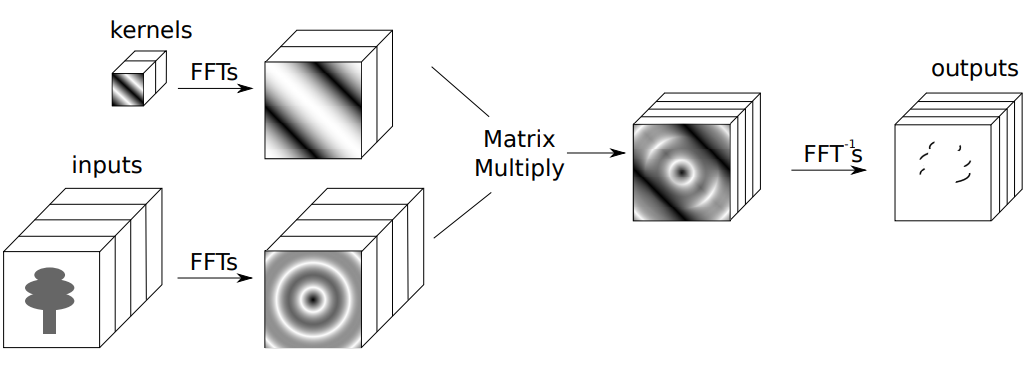
We can compute \(\mathcal{F}(f)\) and \(\mathcal{F}(g)\) in \(\mathcal{O}(N^2\text{log}N^2 + M^2\text{log}M^2) = \mathcal{O}(N^2\text{log}N^2)\) time.

Then, the Hadamart product involves \((N^2)\) operations.

Finally, the inverse FFT requires \(\mathcal{O}(N^2\text{log}N^2)\) time. Thus, we reduce the time complexity of the convolutional layer from \(\mathcal{O}(N^2M^2)\) to \(\mathcal{O}(N^2\text{log}N^2)\).

Pratt et. al. propose such a CNN architecture, which they term Fourier convolutional neural networks (FCNN). The traditional "sliding window" approach to convolutional filtering is replaced by computations of the FFT entirely in the frequency domain.

FCNNs also allow kernel sizes to be learned. In a typical neural network, kernels have fixed size and the network learns only the kernel weights. Since all the operations can now be carried out in the frequency domain, we do not compute the convolutions directly. In an FCNN, kernels can have arbitrary size, limited only by the initial image size. So, a Fourier CNN can not only learn the kernel weights but also the kernel size [5].

References

1. Bishop, Christopher M. Pattern Recognition and Machine Learning. Singapore: Springer Science+Business Media, LLC, 2006.
2. Cooley, James W., and Tukey, John W. "An Algorithm for the Machine Calculation of Complex Fourier Series." Mathematics of Computation, 1965, 297-301. doi:10.1090/S0025-5718-1965-0178586-1.
3. Heideman, M., D. Johnson, and C. Burrus. ”Gauss and the History of the Fast Fourier Transform.” IEEE ASSP Magazine 1, no. 4 (1984): 14-21. doi:10.1109/massp.1984.1162257.
4. Mathieu, Michael, and Mikael Henaff. ”Fast Training of Convolutional Networks through FFTs.” arXiv:1312.5851v5 [cs.CV], March 6, 2014.
5. Pratt, Harry, Bryan Williams, Frans Coenen, and Yalin Zheng. ”FCNN: Fourier Convolutional Neural Networks.” Machine Learning and Knowledge Discovery in Databases Lecture Notes in Computer Science, 2017, 786-98. doi:10.1007/978-3-319-71249-9 47.
6. Stein, Elias M., and Rami Shakarchi. Princeton Lectures in Analysis: Fourier Analysis. Princeton: Princeton Univ. Press, 2003.